You may wonder how each of these transformations works. How does attaching the specified parameter re-shape the rule f in the manner indicated by the graphs?
The transformations aren't very difficult to understand, and they provide good practice in thinking about functions as very general input-to-output processes.
Suppose we are given f . Graphically, we obey the rule y = f(x) as follows:
First, find the input x on the x-axis. Next, compute the output value y using the rule for y = f(x) . Finally, plot a single point at a distance y directly above (or below, if the output y is negative) the position of the input x on the x-axis.
This process produces one point on the graph of y = f(x) for each input x .
Here's how the process changes when we transform the rule with parameters:
-
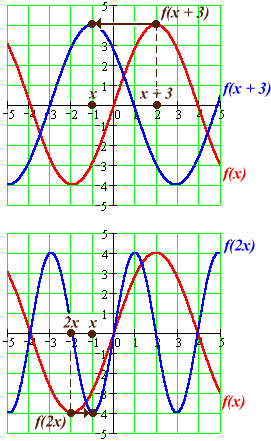
Horizontal Shifts f(x ± a)
& Stretches/Crunches f(ax)
We obey these rules as follows:
First, find the input x on the x-axis.
Next, move along the x-axis to a new position: either x ± a or ax , depending on the case.
At this "new" place on the x-axis, compute the output value y using the input-output rule for f .
Finally, plot a point at a distance y directly above (or below) the position of the original input x — not above (or below) the "new" x value.
The net effect of this process is to grab the output value at the "new" x and "pull it over", so that it is graphed above the original input x .
The only difference between a shift and a stretch/crunch is that for a shift, all values get "pulled over" by the same amount, and for a stretch/crunch they get "pulled over" by an amount that is proportional to the size of the input x.
|
|
-
Vertical Shifts f(x) ± a
& Stretches/Crunches af(x)
The situation is very similar to the cases just described, except that the "pulling" of values is vertical rather than horizontal.
We obey these rules as follows:
First, find the input x on the x-axis.
Next, compute the output value y = f(x) using the input-output rule for f .
Don't plot this y value above (or below) x ...
Instead, locate a new y value at a distance of y ± a or ay above (or below) x , depending on the case. Plot this point.
The net effect of this process is to grab the original output value and "pull it up" (or down) to a "new" output value.
The only difference between a shift and a stretch/crunch is that for a shift, all values get "pulled up" by the same amount, and for a stretch/crunch they get "pulled up" by an amout that is proportional to the size of the original output y.
|

|
Get it? If you do, you probably have a very good understanding of functional input-output rules. Thinking in these terms will help you to use transformations to modify "known" functions into rules that describe entire families of "similar" situations.

