Click here to open an associated Mathcad worksheet:

One way that we use compositions in application is to model physical processes that involve feedback. Feedback refers to situations where a process is executed, and then the output is recycled back to the same process as a new input.

You've no doubt heard feedback if you've ever listened to an electric guitar player place her guitar in front of an amplifier. The sound from the amplifier vibrates the strings on the guitar (just as it vibrates your eardrums) and, through the guitar's pick-ups, it is sent right back into the amplifier. Whatever the input-output behavior of the amplifier (this depends on the cicuitry, and how it is tuned), the process of input-to-output-to-input is repeated again and again and again in a fraction of a second.

Processes that involve repetitions of a set sequence of steps are called iterative. Each cycle in the process is called a loop or an iteration.

Feedback, and iterative processes, are common in mathematics. Many mathematical procedures involve a repetition of the same step, over and over and again, until a satisfactory output is achieved. If the single step can be described by a function, then the process is just one of composing that function with itself repeatedly.

Iterative compositions of the form  ...f(f(f(f(x))))...  would be very tedious for us to compute by hand. Computers, on the other hand, happily perform whatever tedious, iterative tasks we prescribe for them.

Sometimes the result of an iterative computation is the equivalent of the loud shriek that is heard when a guitar is thrust into an amplifier: The successive outputs grow and grow and grow... We may frown on such computations, since they never "settle down" to a result that will allow for further computations outside of the loop. Such runaway processes are said to diverge.

Divergence, however, isn't the only possible outcome of a feedback loop. Try the following. Enter any number you please into a calculator. Now compute the cosine of that number by hitting the appropriate key. (Make sure the calculator is set to work in radians, not degrees.) Compute the cosine of the result. Again. And again. And again... What do you notice? Try it with another input. This feedback loop always "settles down" to a fixed output: 0.739085... We say that this process is convergent.

The following graph of the cosine function, showing repeated compositions with itself, gives you a picture of what is going on here. Note that  cos(x) = x  exactly when  x = 0.739085...

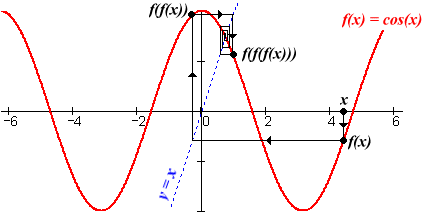
Surprisingly, these two behaviors — divergence to infinity and convergence to a fixed output — don't begin to describe all of the possibilities for a feedback loop. Skilled guitar players know this. They tune their amplifiers, and adjust the timing of the feedback interval by moving their guitars back and forth, until the feedback becomes a part of the music itself.