Inverse Functions

Click here to open an associated Mathcad worksheet:

If we say "I dress for the weather" we mean that what we wear each day is a function of external atmospheric conditions. We certainly don't mean that the weather is a function of what we wear!

The word "function", in everyday use, is one-way: It means something is determined by another thing, but not necessarily vice-versa. The same holds true of mathematical functions: The output must be uniquely determined by the input, but not necessarily vice-versa.

For example, consider the two power functions:

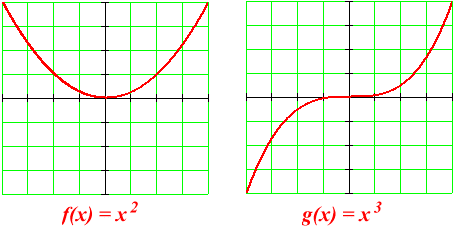
Both functions pass the so-called vertical line test: A vertical line drawn anywhere on the graph crosses the curve at most once. This tells us that for each input there is a unique corresponding output. This is simply the definition of "function".

On the other hand, only the second function, g , passes the so-called horizontal line test: A horizontal line drawn anywhere on the graph of  g  crosses the curve at most once. With  f , it may cross more than once.

What does this tell us about the difference between these two functions?

Only this: The function  g  is invertible, while the function  f  is not. This means that with  g  we may begin with an output value and work our way backwards to find the unique input that produced it. We can't do this with  f .

This is apparent if we examine the two functions algebraically. There are two square roots of any given non-negative number, but there is only one cube root:

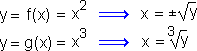
We say that the cube root function is the inverse of the cube function. The square function is not uniquely invertible, so it does not have an inverse function.

In the natural world, some relationships are invertible and some are not. As a result, we sometimes use invertible functions to model what we observe, sometimes not.

Consider, as a domain of inputs, the days of the year. Many things are uniquely determined each day, and so are functions of the day of the year. For example, in any given year the number of bagels consumed in the U.S. is a function of the day. So is the cumulative annual total.

The number of bagels eaten from day to day may fluctuate, with the same number of bagels being eaten on many days during the year. The output (bagels eaten) does not uniquely determine the input (day). The function is not invertible.

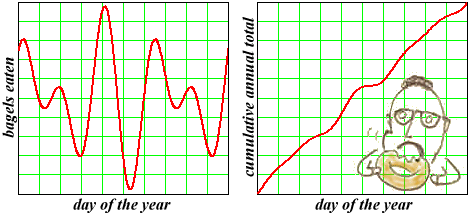
The cumulative annual total, on the other hand, can never decrease. Bagels eaten one day can not be uneaten the next. The total never remains constant either, since someone (let us safely assume) eats a bagel each day. The cumulative total can do only one thing as the days go by: increase. As a result, this function is invertible. Each output (cumulative total) uniquely determines, in reverse, the input (day).

To be invertible, a function's outputs must each correspond to a unique input. A plot of the function must pass the horizontal line test. Only two types of function will qualify: those that are always increasing or those that are always decreasing. Staying level, or fluctuating up and down, rules out the existence of an inverse function.