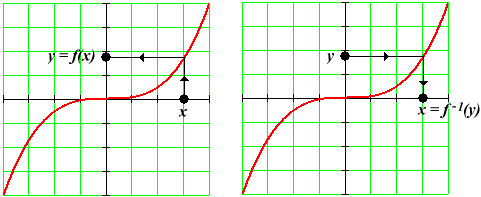
If a function is invertible, then there must be a rule to follow from an output value back to the unique input that produced it. Following this "backwards" rule, of course, will generally be quite different than following the "forward" rule. The inverse, if it exists, is a brand-new function.

When it exists, we give the inverse of a function  f  the name  f ^–1, read "f  inverse". Thus, if  y = f(x)  is invertible, we write  x = f ^–1(y) .

In the plot above,  f(x) = x³  and  f ^–1(y) =  .

WARNING:  f ^–1(y)  does not mean  1 / f(y) . The notation can be a bit confusing, but  f ^–1  is supposed to be a single symbol naming the inverse function, not the reciprocal of the forward function. If, for any reason, we wish to discuss  1 / f(y) , we write  [f(y)] ^–1 .

Notice that, since  f  and  f ^–1  "undo" one another, we always have:

x = f ^–1(f(x))  and  y = f(f ^–1(y))

If  f  is the "poison", then  f ^–1  is the "antidote" when applied in composition.

  The Algebra of Inverses