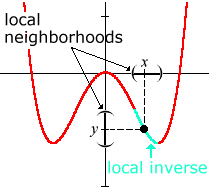
Even when a function does not have an inverse globally (that is, when its full graph fails the horizontal line test), it may have an inverse locally (some part of the graph may pass the horizontal line test). In these cases, we can confine our attention to a "neighborhood" around a point of interest, and speak of the "local inverse":

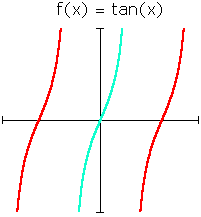
This is the strategy employed when defining the inverse trigonometric functions.

The individual trigonometric functions have an especially nice property: It is possible to find a local inverse function (the principal branch) that works for all invertible  y  values:

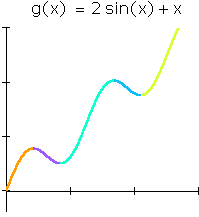
Typically, however, we will have to choose different local inverses for different "areas of interest":

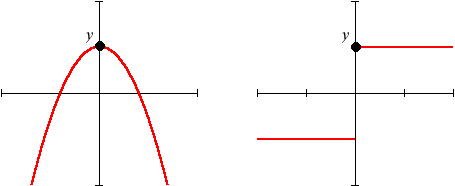
Sometimes local inverses do not exist. The  y  values shown below have no "neighborhoods" for which a local inverse may be defined:

Finding a local inverse near a point depends entirely on whether or not there is a neighborhood of that point in which the function is either strictly increasing or strictly decreasing. The precise conditions under which this is possible are summarized in something called the Inverse Function Theorem, which you'll learn about in calculus.