Implicit Functions

Click here to open an associated Mathcad worksheet:

We're used to seeing algebraic definitions of functions in which the output  y  is given explicitly in terms of some combination of the input  x :

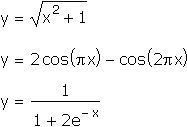
We think of these rules as accepting the input  x , going through a series of steps that transform  x , and then announcing the final result as  y . The output  y  is not involved in the "business" of computing the function, it is only the end product.

What, then, do we make of equations like this:

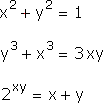
Here the  x s  and  y s  are all mixed-up together, on either side of the equation. There is no obvious way to proceed from an "input"  x  to an "output"  y . It isn't even clear if each  y  is actually a function of the corresponding  x .

We could, of course, attempt to solve each of these equations for  y , writing  y  explicitly as a function of  x , and so try to put ourselves back on familiar ground. In all three cases, however, we will fail.

Sometimes the reason we will fail is that  y  is not uniquely determined by the value of  x : many  y s  will balance the equation when we plug in a particular  x. (For example, solving the first equation for  y  leads to   .) Sometimes the reason is a failure of algebra itself: we can not solve for  y ; it is just too mixed-up with the  x s  for us to be able to extract it. (Try, for example, to solve the last equation for  y .)

The  y s  in such "mixed-up" equations are often called implicit functions of  x . Using the word "function" here is tricky, because, as we have seen, there may in fact be many  y s  corresponding to a particular  x . What is "implicit" (the dictionary defines this as "implied or understood although not directly expressed") is the understanding that many functions may be lurking in such equations, if only we could coax them out.