When can an equation involving  x  and  y  be solved explicitly for  y  as a function of  x ? When does the equation implicitly define several functions of  x ? When does the equation define no functions at all?

To see how we might answer these questions, consider again the equation:

If we pick any point  (a, b)  on the graph of the equation, then (so long as  a ¹ ±1) we can find neighborhoods  A  and  B  of  a  and  b , respectively, with the following property:

If  x Î A , there is a unique  y Î B 
such that  (x, y)  solves the equation.

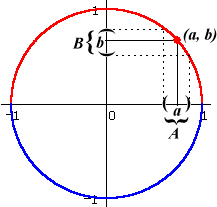
We can therefore define a function  f  with inputs in  A  and outputs in  B  such that  (x, f(x))  solves the equation.

We see that, as for inverse functions, the implicit functions defined by an equation are generally local functions, not global ones. In some instances we may get lucky and be able to solve an equation for  y  explicitly as a single, global function of  x . In these instances we may speak of "the" function defined by the equation (just as we may sometimes speak of "the" inverse). Generally, however, we will only be able to talk about the various functions that are implicitly defined by an equation if we say where we are looking, in terms of neighborhoods of particular inputs and outputs.

Given an equation and input/output neighborhoods "of interest", when will we be able to find an implicitly defined function  f  between those neighborhoods with the property that  (x, f(x))  always satisfies the equation? The answer lies in the Implicit Function Theorem, which you will study in calculus. For now, content yourself with an understanding of how implicitly defined functions may arise.