Just as there are vector quantities which cannot be adequately described by a scalar, there are quantities – or, perhaps more appropriately, situations – which are not adequately described by a single list of numbers. When a situation requires several lists for its description, we often arrange those lists into a matrix.

Here is an example. In mathematics, the term graph has several meanings. One kind of graph, with which you have become well-acquainted in precalculus, displays lists of coordinates, such as the input-output pairs determined by a function. We sometimes call these sorts of graphs plots.

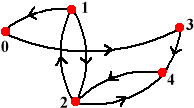
Another kind of graph appears in the description of many applied problems. This sort of graph consists, again, of a collection of points – called nodes in this setting – together with a collection of edges, which connect, or "associate," certain nodes:

This sort of graph appears in descriptions of, for example, telephone networks, airline scheduling, and the phylogeny of biological organisms. Notice that the edges may be directed with arrows, as above. Directed graphs help us to visualize associations that involve potentially one-way relationships, such as "is the sister of".

As useful as graphs may be for visualization, it isn't obvious how to describe them in purely numerical terms. However, this is essential in practical applications such as telephone networking, where graphs can involve millions of nodes and edges. Graphs must be translated to numerical formats that computers can work with.

One method is to use adjacency matricies. The adjacency matrix for the above graph looks like this:

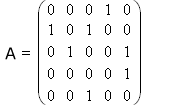
The entry  A_{i, j}  in the ith row and jth column is 1 if node i connects to node j, 0 otherwise. Notice that any single row or column (i.e. vector) describes only the associations of a single node. To describe the entire graph as a single object we need a group of rows – a matrix.

  Explore adjacency matricies

How you use matricies depends on your interests. Their versatile ability to provide numerical descriptions of general relationships, however, make them as ubiquitous in applied mathematics as scalars and vectors.