Power Functions

Modeling Representation

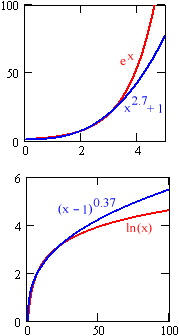Power functions can be difficult to recognize in modeling situations. The reason is that, for long stretches of data, trends modeled by power functions can look like those modeled by exponential and logarithmic functions. The differences between power models and exponential or logarithmic models can be subtle, and emerge only gradually as data accumulates.

The good news is that, when the differences between the various models are so small, it doesn't matter which one is used. This is especially true if our goal is to interpolate values between known data points. Difficulties arise only when we attempt to extrapolate far beyond a data set. Power models slowly diverge from similar-looking exponential or logarithmic models, and what works as a model in the short-term may miss long-term trends.

A classic example is the data on the spread of the HIV virus. Early in the epidemic, the number of cases over time looked essentially like exponential growth. In fact, a power function gave a closer match to the data. Using the exponential model led to overestimates of the number of cases expected in coming years, and resulting overestimates in necessary hospital space, drug production, etc.

So how do we distinguish power functions? What do we look for in a data set to tell us that we are dealing with a power function and not an exponential or a logarithm?

Unfortunately, there is no simple answer. Exponential functions increase by multiples over constant input intervals. Logarithms increase by constant intervals over input multiples. Either of these trends is recognizable in a data set. With power functions, perhaps the best that we can say is that they don't follow either of these patterns.

Power functions model increases and decreases that do not follow exponential or logarithmic data trends.

Power functions follow power trends. There is no simple way to put "power trend" into words – it is just what power functions do. Power trends will always, eventually, outgrow any logarithm. Similarly, powers will always, eventually, undergrow any exponential. "Eventually," however, may be beyond our data set.

In practice, we should try a power fit whenever data appears to have an exponential or logarithmic trend. The model with the best least squares fit is the winner, within the known data. Future trends must be predicted with caution, and models must be re-evaluated when new data becomes available.

Here are some places to look for powers:

• Areas. (area vs. length)
  
  
• Volumes. (volume vs. length)
  
  
• A draining bathtub. (volume vs. time)
  
  
• A falling object. (height vs. time)
  
  
• Light from a bulb. (intensity vs. distance)
  
  
  
• Musical intervals. (frequency vs. number of keys)