Power Functions

Algebraic Representation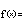

f(x) = a x b

It is easy to confuse power functions with exponential functions. Both have a basic form that is given by two parameters. Both forms look very similar. In exponential functions, a fixed base is raised to a variable exponent. In power functions, however, a variable base is raised to a fixed exponent.

The parameter  a  serves as a simple scaling factor, moving the values of  x^b  up or down as  a  increases or decreases, respectively

The parameter  b , called either the exponent or the power, determines the function's rates of growth or decay. Depending on whether it is positive or negative, a whole number or a fraction,  b  will also determine the function's overall shape and behavior.

More so than other simple families like lines, exponentials, and logs, members of the power family can exhibit many distinctive behaviors.

Notice that when  b = 0  the function simplifies to  f(x) = ax⁰ = a1 = a , a constant function with an output of  a  for every input. When  b > 0 ,  f(0) = a0^b = 0 . That is, every power function with a positive exponent passes through  (0, 0) . When  b < 0 ,  f(0)  is undefined. (Remember,  x^–b = 1 / x^b .) Thus, power functions with negative exponents have no y-intercepts. Power functions with negative, whole number exponents like  x^–1  or  x^–2  are simple examples of rational functions, and for these functions  x = 0  is an example of a singularity.

To appreciate the variety of behaviors among members of the power family, consider two simple cases:

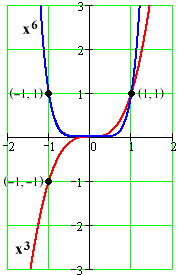• Even powers.
  
  If  b  is a an even whole number like  b = –2, 4, 10, etc., then for any input  x  we will have  f(–x) = a(–x)^b = a(–1)^b(x)^b = a(x)^b = f(x) , since  –1  raised to an even power is  1 . The function has a certain symmetry: Its outputs for any  x  are exactly the same as its outputs for  –x . We call any function with this behavior an even function, with even powers serving as the archetype.
  
  
• Odd powers.
  
  If  b  is a an odd whole number like  b = –1, 3, 7, etc., then for any input  x  we will have  f(–x) = a(–x)^b = a(–1)^b(x)^b = a(–1)(x)^b = –f(x) , since  –1  raised to an odd power is  –1 . The function has a certain anti-symmetry: Its outputs for any  x  are exactly the opposite of its outputs for  –x  . We call any function with this behavior an odd function, with odd powers serving as the archetype.

The difference between odd and even powers only hints at the differences among power functions.

Another helpful distinction separates functions with whole number (integer) powers from those with fractional powers. (We leave the consideration of irrational powers to calculus.)

• Integer powers.
  
  We've already noted the symmetry/anti-symmetry of even/odd integer powers. There is also a key difference between positive and negative integer powers. We've noted that all positive powers pass through  (0, 0), while all negative powers have a singularity at  x = 0 . When we put together the even/odd possibilities with the positive/negative possibilities for integer powers, we find four distinct cases for growth and decay.

  Cases for integer powers:
  
  

• Fractional powers.
  
  It doesn't make any sense to distinguish between "even" and "odd" fractional powers – those terms refer only to integers.

  It does makes sense to talk about positive and negative fractional powers, however, and this distinction is again important in determining overall behavior.

  Another distinction – a new one – also comes into play when we consider fractional powers. Suppose that the fractional power  m/n  has been reduced to lowest terms (all common factors in the numerator and the denominator have been cancelled). To calculate  x^m/n, we proceed in two steps: 1) Find the  n ^th  root of  x  (x^1/n = 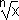); 2) Raise it to the  m ^th  power. The second step is straightforward: We can raise any number to an integer power. The first step, however, is problematic for negative  x : We can not meaningfully ask for an even root of a negative number. Thus, the allowable inputs (domains) of fractional powers depend on whether  n  is even or odd.

  Considering this in combination with the positive/negative possibilities, we once again find four distinct cases for growth and decay (each with several sub-cases).

  Cases for fractional powers:

It is difficult to single out one key    algebraic property of power functions from all of this variety. Perhaps it is best to say simply that powers behave like powers, with an appreciation for the many different behaviors that this can encompass.